En etkili bilimsel denklemleri hesaplamak hiç de kolay bir iş değil ancak bu beş denklem kesinlikle en üst sıralarda yer alıyor.
Denklem nedir, hiç düşündünüz mü? Harfler, sayılar, garip semboller, gizem ve çözüm. Hepsi aynı anda bir denklemin içerisinde olabilir.
Binicisini bekleyen bir at gibi denklemlerde adeta mucidini beklerler. Fiziksel gerçekliğin temel bileşenleri arasındaki ilişkilere yeni bir bakış açısı ile bakmak gerekir. İster kütle ve enerji arasındaki ilişki olsun ister iki cisim arasındaki çekim kuvveti isterse de bir üçgenin kenarlarının ölçülerinin hesaplanması olsun, tüm denklemler evrenle ilgili önemli bir bilimsel gerçeği kristalize eder. Her bilimsel analiz, bizi evrenin bilinmeyen sırlarının çözümüne biraz daha yaklaştırır.
Herhangi bir denklemin en önemli kısmı, kalbindeki eşittir işaretidir. Bu iki yatay çizgi, bir şeyi değiştirdiğimizde, görünüşte ayrı olan başka bir şeye karşılık gelen bir değişiklik ile karşılaşacağımızı söylemektedir. Bu şekilde, denklemler yüzeysel olarak farklı nicelikler veya özellikler arasındaki bağlantıları ortaya çıkarır. Bir kez birbirine bağlandıktan sonra, yeni keşfedilen ilişkiler gelecekteki araştırmalar için temel teşkil edebilir.
En önemli denklemleri fark edebilmek ve çözüme gidebilmek neredeyse umutsuz bir iştir. Çünkü herhangi bir ilişkinin önemi, bağlama bağlı olarak büyük ölçüde farklılık göstermektedir. Örneğin bir uçaktan düşüyorsanız, yerçekimi yasası size Newton’un yer çekimi yasasından ve Schrödinger denkleminden çok daha fazla ve önemli hisler hissettirecektir! Benzer şekilde denklemler bilim insanları için bulundukları alanlara göre farklı önemler taşır.
Dünyayı görme şeklimiz yani nasıl gördüğümüz üzerinde büyük etkisi olan bazı denklemleri seçmek ile mümkündür. Bu denklemlerin tümü, bir kez kâğıda döküldüğünde, asırlar ve nesiller boyu düşünerek kâinatın sırlarını çözmek için büyük bir heyecan duyan bilim insanlarının güçlerini yeni keşifler yapmak için kullanmalarını ve birbirlerinin bulgu ve teorilerinden faydalanmaları sonucunda mümkün olmuştur. Örneğin E=mc^2 formülünde enerjinin kütle ile ışık hızının çarpımına eşit olmasının keşfedilmesi başarısında olduğu gibi.
E = mc²
Verdiğimiz bu örnek insanlık tarihinin gördüğü en ünlü denklemlerden birinin çözümüdür. Albert Einstein’ın kütle ve enerjiyi ilişkilendiren 1905 tarihli denklemidir. Hem zarif hem de yüzeysel olarak mantığa aykırı gibi gözükmektedir. Enerjinin, durgun çerçevesindeki bir nesnenin kütlesinin ışık hızının karesiyle çarpımına eşit olduğunu söyler. Einstein bunu yaparken, o zamana kadar iki ayrı alanı birleştiren kütle ve enerjinin birbirine eşdeğer kabul edilebileceğini ortaya koyar.
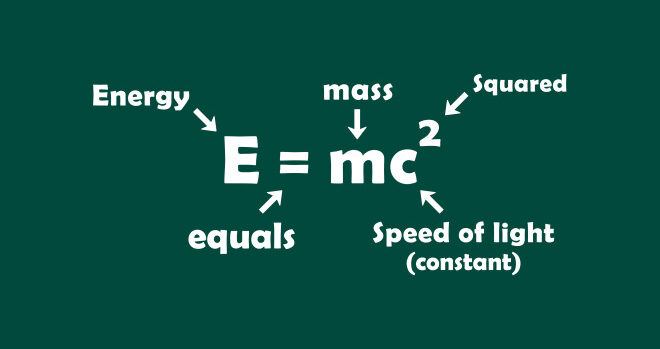
Einstein denklemde, bir nesnenin kütlesini değiştirmenin içerdiği enerjiyi de değiştireceğini söyler fakat kâinatta, bu kanunun tersine işleyen yıldızlar da mevcuttur. Nükleer bir patlama sırasında, radyoaktif elementlerin kütlesinde meydana gelen küçük değişikliklerin büyük miktarda enerjiye karşılık geldiği zaman, korkunç bir şekilde muazzam değişiklikler ortaya çıkabilmektedir.
Denklemin kütlenin enerjiye dönüştürülebileceğini ve tekrar geri dönebileceğini gösterdiğine dair yaygın bir yanlış anlama vardır. Aslında Einstein’ın kastettiği bu değildir. Bunun yerine, değişen kütlenin, çok büyük de olsa, enerjide bir değişiklikle sonuçlanması gerektiğini göstermek istemiştir.
Pisagor Teoremi
Bir dik üçgenin iki ayağı ile hipotenüsü arasındaki bu temel ilişki, Yunan filozofu Pisagor’un adını almıştır ancak bunu ilk bulan kişi o değildir.
Teorem, herhangi bir dik üçgen için onun iki kısa ayağının karesini toplayabileceğimizi ve en uzun ayağının karesini alabileceğimizi göstermektedir. Bu, geometri ve cebir disiplinlerini bir araya getirmiştir. Sayılar hakkında temel bir gözlem elde etmek için şekiller arasındaki ilişkileri kullanmanın iyi bir erken örneğidir. Bu konudaki müteakip keşifler bugün topoloji alanında da yaşanmaktadır. Daha açık bir deyişle, GPS üçgeni konumumuzun belirlenmesinde de kullandığımız Pisagor Teoremi’ne her zaman güvenmekteyiz.
Termodinamiğin İkinci Yasası
Termodinamiğin yasaları, enerjinin nasıl hareket ettiğine dair gözlemlerden ortaya çıkmıştır. Birinci yasa, enerjinin her zaman korunması gerektiğini belirten önemli bir bulgudur. Ancak başlangıçta bir sistemde ısının nasıl aktarıldığını açıklayan ikinci yasanın, olağanüstü derecede geniş kapsamlı sonuçları olduğu sonradan kanıtlanacaktır.
Yasa, duruma bağlı olarak birçok şekilde formüle edilebilir, ancak yaptığı en temel gözlem, ısının ve dolayısıyla enerjinin, sıcaktan soğuğa doğal olarak yalnızca bir yönde aktığıdır. Enerji harcayarak bir şeyi ısıtabilsek de bu sadece geçici bir çözümdür. Bu her gün gördüğümüz bir şeydir ama önemi çok büyüktür. Bu ısı ilişkisi, zamanın oku ve entropi gibi baş döndürücü kavramların altında yatmaktadır. Nihayetinde, kütle ve enerji evrene o kadar ince ve eşit bir şekilde yayılmıştır ki şu anda evrendeki denge inanılmaz derecede uyumludur fakat eninde sonunda bu ısı ve kütle dengesi arasındaki ilişki bozulacak ve evrenin ısı ölümünün kaçınılmazlığı gerçeği ile yüzleşeceğiz.
Kalkülüs
Matematik birçok farklı denklem içerir ancak bir denklem insanlık için çok büyük önem arz eder. İki önemli 17. yüzyıl düşünürü, Isaac Newton ve Gottfried Leibniz, bağımsız olarak, tanımlanmış bir sınıra yaklaştıkça sonsuz serilerin yakınsamasını resmileştirmenin bir yolunu buldular. Bu kısmen, herhangi bir noktada eğri bir çizginin eğimini hesaplamaya çalışma probleminden ortaya çıkmıştır.
Leibniz ve Newton çalışmalarında, kalkülüsün iki temel taşı olan türev ve integrali keşfetmişlerdir. Türevler bize bir fonksiyonun anlık değişim oranını verirler. İntegraller ise grafikte bir eğrinin altındaki alanı verirler. Türevler ve integraller bugün matematik, mühendislik, fizik, ekonomi ve diğer birçok bilimsel disiplinin bir parçasıdırlar.
Bu iki önemli matematikçi, kalkülüsün gerçek babası olarak kimin kabul edilmesi gerektiği konusunda acı bir şekilde anlaşamadılar. Bugün, her ikisi de türev ve integrali birbirinden bağımsız olarak icat etmekle anılmaktadırlar. Yine de matematiksel işlemlerdeki dehası ve önemli çalışmaları için Leibniz’e teşekkür edebiliriz. Her şey Newton’un istediği gibi olsaydı, bugün onun kitabı “Method of Fluxions“ına atıfta bulunurduk.
Evrensel Yerçekimi Yasası
Newton, yerçekimi kanunu keşfi için kendisini ön plana çıkarmış olsa da bu buluş için kendisinden önce önemli çalışmalar yapan bilim insanlarına müteşekkir olmalıdır. Evrensel Yerçekimi Yasası için tek taraflı olarak iddiaları olabilir fakat bu denklem, Galileo ve Johannes Kepler gibi bilim insanlarının, evrendeki bir madde parçacığının, maddenin diğer her parçacığına çekici bir kuvvet uyguladığını belirtmek için yaptıkları çalışmalara dayanmaktadır. Bu kuvvet, kütle ile artar ve mesafe ile üstel olarak azalır.
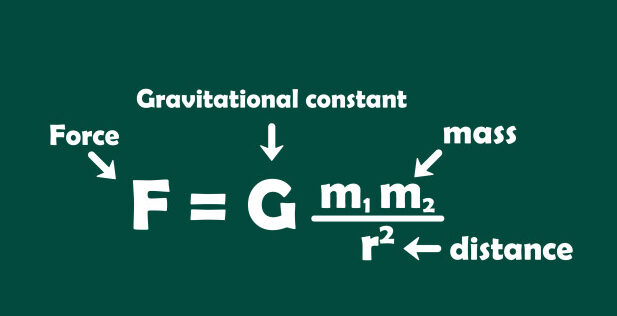
Newton’un çalışması, Galileo’nun Dünya üzerindeki nesnelerin hareketine ilişkin gözlemlerini Kepler’in astronomik cisimlerin hareketine ilişkin çalışmasıyla birleştirdi. Sonuç, aynı kuralların hem gezegenlerin hem de top güllelerinin hareketlerini yönettiğini gösteren bir denklemdi. Onun zamanında olması, kendisi tarafından bulunmuş gibi gösterilmesi bu gerçeği gizleyemez.
Bugün, Newton yasalarının yerini, diğer şeylerin yanı sıra birbirine çok yakın veya çok ağır şeyleri açıklayan Einstein’ın Görelilik Teorisi almıştır. Ancak Newton’un gözlemleri, etrafımızda gördüğümüz etkileşimlerin çoğu için hala geçerlidir. 17. yüzyılda yaşamış birisi için bu çalışma fena değildir.
Yazan: Nathaniel Scharping
Çeviren: Halil İbrahim İşbilici
Kaynak: discovermagazine.com
