Karışıklık (büyük olasılıkla kasıtlı), ilkokulda ve lisede kullanılan matematik kuralları arasında bir tutarsızlığa yol açtı. Son zamanlarda, çevrimiçi bir tartışma yaratmayı başaran bir matematik denklemi hakkında yazmıştım.
Çeviren: Elif Akçay
Denklem şuydu:
8 ÷ 2 (2 + 2) = ?
Mesele matematiksel işlemlerin hangi sırayla yapıldığına bağlı olarak 16 ya da 1 olmak üzere iki farklı cevap üretmesiydi. Genç Matematik öğrencileri belirli bir metottaki işlem sırası için bölündü. Ki bu işlem sırası şuydu: Parantezler, üsler, çarpma ve bölme eşit temelde ele alınıp soldan sağa çalışarak çözülecek, aynı eşit önceliğe sahip toplama ve çıkarma da bağlarından koparılıp çözülecek.
Bu ilkel PEMDAS metoduna sıkı sıkıya bağlı kalmanın, sadece bir cevaba yol açtığını savundum: 16.

Bununla birlikte, standart işlem sırasına eşit derecede bağlı olan birçok editör (kendiminki de dahil), doğru cevabın 1 olduğunu şiddetle ve ısrarla vurguladı. Makaleyle ilgili birçok yorum okuduktan sonra, bu katılımcıların çoğunun makalede tanımladığım ilk PEMDAS sözleşmesinden daha farklı (ve daha sofistike) bir metot kullandığını fark ettim.
Cebirde sıklıkla kullanılan bu daha sofistike konvansiyonda, örtülü çarpma işlemine, açık çarpma işleminden veya açık bölme işleminden (bu işlemlerin açıkça × * / veya ÷ gibi sembollerle yazıldığı) daha yüksek öncelik tanınır.
Bu metot altında, 2 (2 + 2) ‘deki örtük çarpıma 8 ÷2 (2 + 2)’ deki açık bölme işleminden daha yüksek öncelik verilir. Başka bir deyişle, önce 2 (2 + 2) değerlendirilmelidir. Bu da 8 ÷ 2 (2 + 2) = 8 ÷ 8 = 1 demek olur.
Aynı kuralda, birçok yorumcu 8 ÷ 2 (4) ifadesinin 8 ÷ 2 × 4 ile eşanlamlı olmadığını, çünkü parantezlerin hemen çözülmesi gerektiği ve bu nedenle tekrar 8 ÷ 8 = 1 sonucuna varıldığını iddia etmiştir. Bu metot çok makul ve eğer buna uyursak cevabın 1 olduğunu kabul ediyorum. Ancak bu evrensel olarak benimsenmemiştir. Google ve WolframAlpha‘da bulunan hesap makineleri daha basit olan metotu kullanır; basit aritmetik ifadeleri değerlendirme talimatı verildiğinde, üstü kapalı ve açık çarpma arasında bir ayrım yapmazlar.
Ayrıca, Google ve WolframAlpha, bir dizi parantez içinde ne olduğunu değerlendirdikten sonra, parantezleri etkili bir şekilde siler ve artık içeriğe öncelik vermezler. Özellikle, 8 ÷ 2 (2 + 2) ‘yi 8 × 2 × (2 + 2) = 8 ÷ 2 × (4) olarak yorumlar ve bunu 8 ÷ 2 × 4 ile eşanlamlı olarak değerlendirir. Daha sonra, temel PEMDAS’a göre, bölünme ve çarpma eşit önceliğe sahiptir, bu yüzden soldan sağa çalışırız ve 8 ÷ 2 × 4 = 4 × 4 elde eder ve 16 cevabına varırız. Makalem için bu basit metot üzerinde durmayı seçtim.
Diğer yorumcular orijinal sorunun kendisine itiraz ettiler. Ne kadar kötü gözüktüğüne baksanıza; eğer doğru yerlere parantez setleri eklenmiş olsaydı (8 8 2) (2 + 2) veya 8 ÷ (2 (2 + 2)) gibi, daha net anlaşılabilir de olabilirdi. Doğru, ama bir nokta gözden kaçırılıyor; sorunun net bir şekilde bir şey sorduğu söylenemez. Aksine, belirsizliği neredeyse kasıtlı görünüyor. Yaramazlıklara neden olacak şekilde yapılmış gibi, kesinlikle ustaca sapkın.
8 ÷ 2 (2 + 2) ifadesi bulanıklığı daha da artırmak yerine, karışıklığı azaltmak için parantezleri kullanırdı. Bunu, sayı 2’yi ve ifadeyi (2 + 2) yan yana getirerek, çarpmalarının kesin olarak belirtildiğine işaret edip gene aralarına açık bir çarpma işareti koymadan yapardı. İzleyici, karmaşık metodu cebir sınıfında gördüğü gibi örtülü çarpım için kullanıp kullanmayacağını ya da ortaokuldan ilköğretime kadar ki kısımda gördüğü PEMDAS metoduna geri dönüp dönmeyeceğini merak ediyor.
David adlı bir yorumcu, çıkmazı özenle özetledi: “Dolayısıyla, sorun ilkokul ile lise de gösterilen dersleri anlam ifade etmeyecek şekilde birleştiriyor. İlkokul matematiklerini iyi hatırlayanlar cevabı 16, cebir derslerini hatırlayanların ise cevaba 1 demesi daha muhtemeldir.”
Bu soruya açık bir cevabı tercih ediyoruz fakat öyle bir cevap yok. Domates diyorsun, tomahto diyorum. Bazı elektronik tablolar ve yazılım sistemleri soruyu cevaplamayı açıkça reddediyorlar; Bu benim ve konuştuğum çoğu matematikçininki gibi öyle.
Daha net bir cevap istiyorsanız, daha net bir soru sorun.
Yazar: Steven Strogatz
Kaynak: nytimes.com

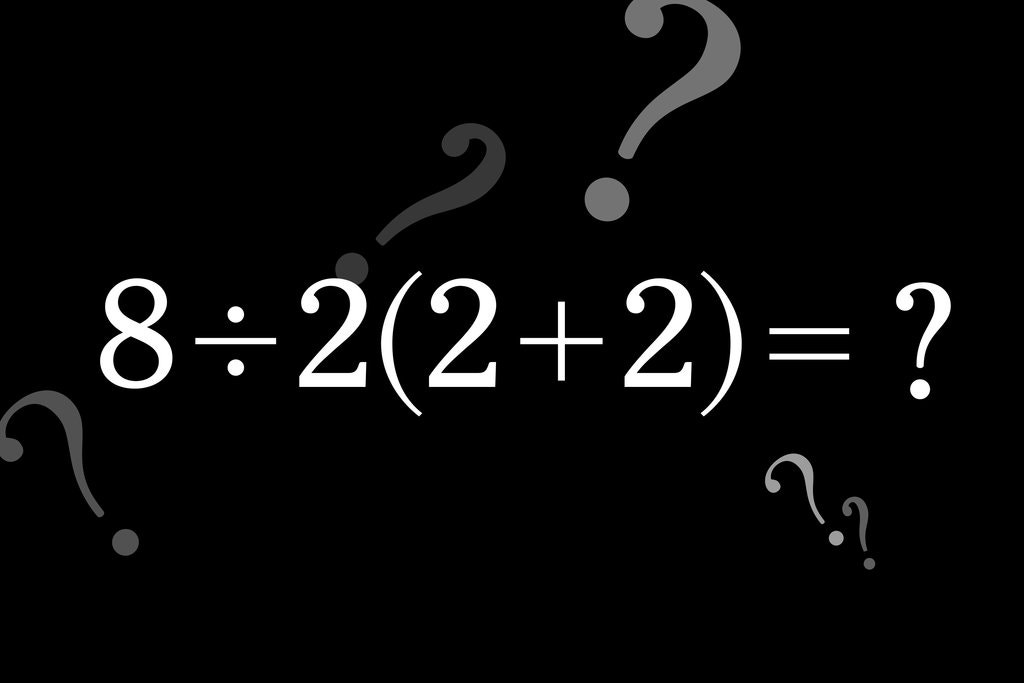




En son iyi bitirmis
Daha net bir cevap istiyorsanız, daha net bir soru sorun.
😀