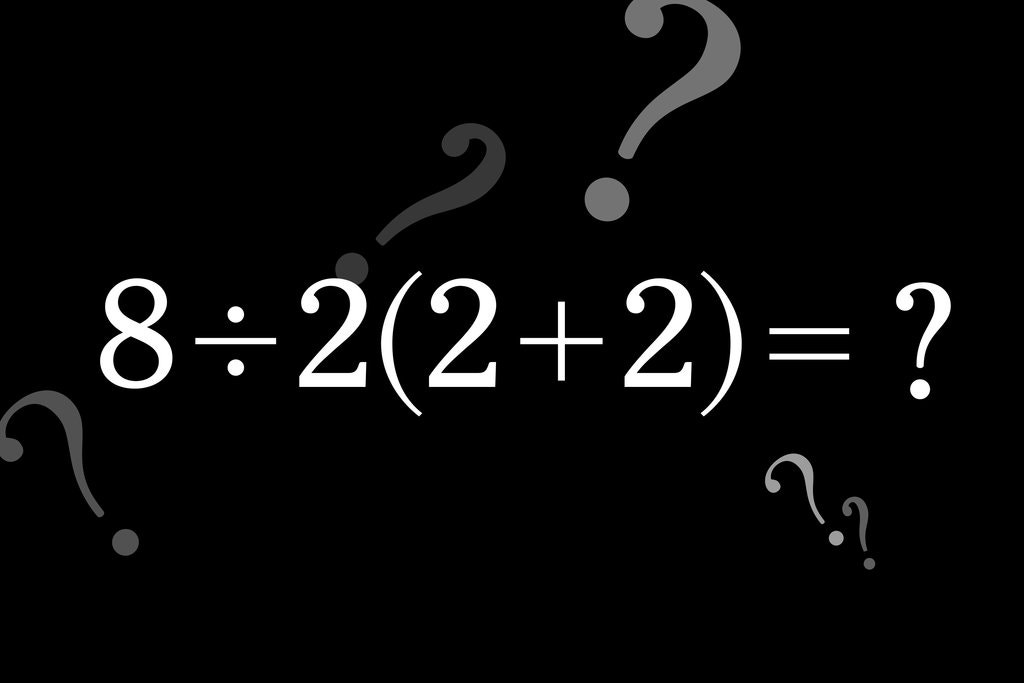Bazen BODMAS başka bir isim ile sadece PEMDAS olur. Ve hayır, cevap 100 değil.
Çeviren: Elif Akçay
Matematiksel Twitter normalde internet ortamı için sessiz ve düzenli bir sığınak. Ancak 28 Temmuz’da durgunluğu altüst etmeye karar veren biri bunu kesin bir provokasyonla yaptı. Bu olayın lise öğretmenlerinin “işlemlerin sırası” olarak adlandırdığı bir şeyle ilgisi var. Basit gibi görünen işte o meşhur soru:
8 ÷ 2(2+2) =?
Birçok yanıtlayan için cevabın 16 olduğu kesindi. Diğerleri ise doğru cevabın 1 olduğunda ısrarlıydı. İşte o zaman saçma konuşmalar başladı. Birileri “Bazılarınızın matematikte başarısız olduklarını gördük” dedi. Bir diğeri, iki farklı elektronik hesap makinesinin bile aynı fikirde olmadığını gösteren bir fotoğraf yayınladı.
Normalde doğru ve yanlışın var olduğu mantığın hakimiyetindeki güven veren matematik dünyası can sıkıcı olmaya başlamıştı.
Hepimiz “işlemlerin sırasını” düzenleyen aynı kurallarla oynamayı kabul ediyorsak yukarıdaki sorunun açık ve kesin bir cevabı var. Bu durumda olduğu gibi- parantez içindeki ifadeleri değerlendirmek, çarpma, bölme veya toplama, çıkarma işlemleri yapmak için- çözüm sıralamasındaki önceliklerimize göre büyük farkların çıkabileceği birçok matematiksel işlemle karşı karşıya kalıyoruz.
Twitter’da ki herkes 8 ÷ 2 (2 + 2) ile karşılaştığında, parantez içindeki 2 + 2 değerinin önce değerlendirilmesi gerektiğini kabul etti. Öğretmenlerimizin bize söylediği şey şuydu: Önce parantez içinde ne varsa onunla ilgilen. Tabii ki 2 + 2 = 4. Yani soru 8 ÷ 2 × 4 seviyesine indi ama asıl sorun şurada: Şimdi de bir bölme ve çarpma ile karşı karşıya kaldık, hangisi öncelikli? Önce bölmeyi yaparsak, 4 × 4 = 16; önce çarpmayı yaparsak, 8 ÷ 8 = 1 olur.
Peki, hangi yol doğru? Standart sözleşme, çarpma ve bölmenin eşit önceliğe sahip olduğunu göstermektedir. Eşitliği bozmak için soldan sağa çalışıyoruz; bölme önce gider, sonra çarpma. Böylece, doğru cevap 16 olur.
Daha genel olarak, geleneksel işlem sırası önce parantez içindeki ifadeleri değerlendirmektir. Sonra üslülerle başa çıkarsın. Daha sonra, dediğim gibi, gelen çarpma ve bölme işlemleri eşit öncelikli kabul edilip belirsizlikler soldan sağa ortadan kaldırılmaya başlanır. Sonra da tekrar eşit önceliğe sahip olan toplama ve çıkarma da soldan sağa çözüme kavuşturulur.
Amerika Birleşik Devletleri’ndeki öğrencilerin bu işlem sırasını hatırlamasına yardımcı olmak için, öğretmenler PEMDAS (parentheses, exponents, multiplication, division, addition, subtraction) kısaltmasını kullanırlar: parantez, üstler, çarpma, bölme, toplama, çıkarma. Diğer öğretmenler eşdeğer bir kısaltma olan BODMAS’ı (brackets, orders, division and multiplication, and addition and subtraction) kullanır: parantez, emir, bölme ve çarpma ve toplama ve çıkarma. Çoğu ise, baş harfleri dikkate alınmalı, “Please excuse my dear Aunt Sally.”i hatırlamalarını ister.
[Bu matematik problemi, internetin ilk bölünmüşlüğü değil. Yanny ve Laurel’i hatırladın mı? Ya da elbisenin rengini herkesin farklı görmesi durumunu?]
Anlıyoruz ki, Sally Teyze tamamen metot meselesi. Bu anlamda, PEMDAS ise keyfidir. Dahası, bir matematikçi olarak deneyimlerime göre, 8 × 2 × 4 gibi ifadeler saçma sapan görünüyor. Hiçbir profesyonel matematikçi, hiçbir zaman, açıkça belirsiz olan bir şey yazmaz. Bölmenin ya da çarpmanın hangisinin öncelikli olmasını istiyorsak oraya bir parantez ekleyerek bunu işaret ederdik.
Bu Twitter’da ortaya çıktığında, öfkeyle tepki gösterdim: Saçma gözüküyordu, lise müfredatımızda bu denli safsatalar için çok zaman harcıyoruz. Ama şimdi, Twitter’da bilgisayar odaklı arkadaşlarımdan bazılarından aydınlanmış olarak, metotların önemli olduğunu ve yaşamların onlara bağlı olabileceğini kabul ediyorum.
Ne zaman yola çıkacağımızı biliyoruz. Eğer herkes yolun sağından gidiyorsa (Amerika’daki gibi), biz de diğerlerini takip ederiz çünkü akıllıca olan budur. Aynı şey eğer yol soldan akıyor olsaydı (Birleşik Krallık’taki gibi) burada da geçerli olacaktı. Herkes takip ettiği sürece, hangi metodun kabul edildiğinin bir önemi yoktur.
Aynı şekilde, bilgisayarlar, elektronik tablolar ve hesap makineleri için yazılım yazan herkesin işlem sırasına ilişkin kuralları bilmesi ve bunları takip etmesi esastır. Geri kalanımız için PEMDAS’ın karmaşıklığı, metotların yer aldığı geniş derslerden daha az önemlidir. Onlar yolun ortasındaki birbirini anlayıp birlikte çalışan ve kafa kafaya çarpmaktan kaçınan çift sarı çizgidir, bitmeyen bir eşittir işareti gibi.
Sonuçta, 8 ÷ 2 (2 + 2) sözlü saldırıdan daha düşük bir ifadedir. Bu bir nevi “Eats shoots and leaves*” ifadesini yazmak gibi. (*Orijinalinde de “Yiyor, Sürgünler ve Yapraklar” gibi virgül olması gerektiği vurgulanıyor.) Evet, noktalama işaretlerini bu yüzden icat ettik.
Bu yüzden, tüm matematik öğretmenleri adına yazıyorum ki gençlerimiz bu can sıkıcılıktan ötürü bizi affetsin. Kızlarım, eğitim süreleri boyunca her okul yılında haftalarını sanki birer otomat olmak için geçirdiler. Şüphesiz, birçok öğrenci matematiği insanlık dışı, anlamsız bir keyfi kurallar ve prosedürler bütünü olarak görmeye başlar.
Açıkçası, internetteki bu son karışıklık herhangi bir şeyi gösteriyorsa o da birçok öğrencinin daha derin ve temel dersleri özümseyemediği olmuştur. Belki de sevgili Sally Teyze mazeretini bir kenara bırakıp onu kucaklamanın zamanı gelmiştir. Daha da iyisi herkese belirsizliğe yer vermeyen matematik ifadeleri yazmayı öğretmek olmalı ve sonra tüm bunlar ortadan kalkacaktır. Yazılım tasarımcısı olmayı hedefleyen öğrenciler için belirsiz ifadeler ortaya çıktığında güvenle kullanabilecekleri kod yazmak Sally Teyze’yi mezarından çıkarmakla mümkün gibi görünüyor. Diğer herkes için, öğrencilerimize matematiğin güzelliğini, ilginç ve canlandırıcı kısımlarını öğretmek için daha fazla zaman harcayalım. Matematik daha iyisini hak ediyor.
Steven Strogatz: Cornell’de Matematik Profesörü ve “Sonsuz Güçler: Calculus Evrenin Sırlarını Nasıl Açığa Çıkarır?” adlı kitabın yazarı.
Kaynak: nytimes.com
